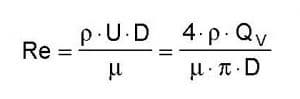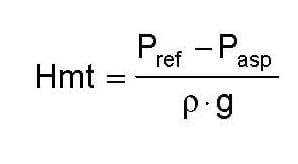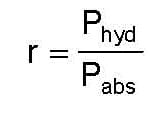I/ RAPPELS DE STATIQUE DES FLUIDES

1 / Unités de pression

Plusieurs unités existent:

• le pascal (Pa) : unité SI, peu employée en pratique
• le bar (bar) et son sous multiple le millibar (mbar)
• le millimètre de mercure ou Torr
• le millimètre de colonne d’eau ou le mètre de colonne d’eau (m CE)
• l’atmosphère (atm)

La correspondance entre ces unités est la suivante:

1 bar = 10⁵ Pa =  1000 mbar ≈ 750 mm de mercure ≈ 10,2 m CE ≈ 0,987 atm

La pression atmosphérique est la pression exercée par l’atmosphère à la surface de la terre. Au niveau de la mer cette pression est équivalente à celle exercée par une colonne d’environ 760 mm de mercure. Elle varie tous les jours légèrement : elle est néanmoins toujours voisine de 1 bar.

2 / Pression absolue et pression relative

La pression absolue est la pression mesurée par rapport au vide absolu (c’est à-dire l’absence totale de matière). Elle est toujours positive.

La pression relative se définit par rapport à la pression atmosphérique existant au moment de la mesure : cette pression peut donc prendre une valeur positive si la pression est supérieure à la pression atmosphérique ou une valeur négative si la pression est inférieure à la pression atmosphérique.

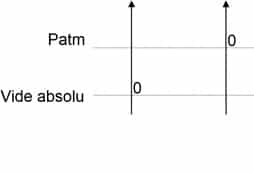
échelle pression absolue        échelle pression relative

Les deux types de pressions correspondent physiquement à la même pression, elles sont simplement exprimées sur des échelles ayant des “zéros” différents. La relation suivante permet de passer de l’une à l’autre :

Pabsolue = Prelative +Patmosphérique

On parle parfois de pression différentielle : il s’agit de la différence de pression mesurée entre deux points. Cette différence a évidemment la même valeur pour des pressions exprimées en pression absolue ou en pression relative.

On parle de dépression quand la pression absolue est inférieure à la pression atmosphérique : la pression relative est négative dans le cas d’une dépression.

Les formules établies par la suite font toutes référence à des pressions absolues.

3 / Mesures de pression

Dans l’industrie chimique, on mesure en réalité dans la grande majorité des cas des pressions relatives ce qui est suffisant. On s’intéresse également souvent à des différences de pression entre deux points.

Les moyens de mesure utilisent dans leur principe la comparaison par rapport à la pression atmosphérique: ceci justifie donc la définition des pressions relatives.

Il existe deux catégories principales d’instruments de mesures de pression :

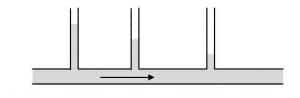
• les manomètres à tubes en U:

Pour une mesure de pression relative ils sont ouverts à l’atmosphère à une de leurs extrémités et remplis par un liquide (couramment eau ou mercure). L’autre extrémité est reliée à l’enceinte dont on veut connaître la pression relative. Pour une mesure de pression différentielle les deux extrémités du tube sont reliés aux deux points entre lesquelles on cherche à connaître la pression différentielle. La mesure se lit dans les deux cas directement par différence de niveau du liquide dans les deux branches de tube.

L’utilisation de l’eau ou du mercure est fonction du but poursuivi: l’eau convient mieux pour de faibles pressions (inférieures à 0,1 bar) grâce à une bien meilleure précision. Par contre le mercure s’impose pour des valeurs supérieures à cause de la trop grande taille des tubes nécessaires.

• les manomètres métalliques: type manomètre de Bourdon

Suivant la pression du liquide à l’intérieur du tube métallique, celui-ci va augmenter ou diminuer son rayon de courbure et ce de manière plus ou moins importante en fonction de la valeur de l’écart entre la pression mesurée et la pression atmosphérique ; l’aiguille solidaire du tube se déplace donc en fonction de la pression mesurée.

4 / Principe fondamental de l’hydrostatique

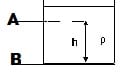
On considère un liquide immobile à l’intérieur d’un récipient; la pression en tous les points du liquide situés sur un même plan horizontal est identique. Les points A et B étant sur une verticale, le principe s’écrit:

P_B − P_A = ρ⋅ g⋅ h

PB, PA : pressions en B et A	→	kg/(m.s2)   ou Pa (pascal )
ρ : masse volumique du liquide	→	kg/m3
g : accélération de la pesanteur	→	m/s2
h : distance verticale entre A et B	→	m

 

La différence de pression (en Pa) entre A et B est numériquement égale au poids d’une colonne de liquide de section unité 1 m² et de hauteur h en m:  on pourra dire que P_B – P_A  exprimée en pascals est donc égale à une pression de h m de colonne de liquide de masse volumique ρ (kg/m³) . On peut toujours exprimer une pression avec une unité de hauteur après avoir précisé le liquide choisi.

remarque:  la relation de Bernoulli est une formulation plus générale qui prend en compte la statique des fluides.

II/ NOTIONS IMPORTANTES DE LA MÉCANIQUE DES FLUIDES

La mécanique des fluides s’intéresse à l’écoulement des fluides. Nous supposerons toujours que le régime permanent est atteint, que la longueur des canalisations est infiniment plus grande que leur section et que la température est constante tout au long de l’écoulement. On admettra également que les canalisations où circulent les liquides seront toujours remplies totalement.

On admet que la pression est uniforme dans une section perpendiculaire à l’axe de l’écoulement.

1 / Fluides compressibles et incompressibles

Un fluide incompressible est un fluide dont la masse volumique ρ est constante, indépendante de la pression P. Un fluide compressible est un fluide pour lequel il faut tenir compte des variations de ρ avec P. Dans la pratique on nomme fluide incompressible un fluide pour lequel ρ est indépendante de P et de la température θ.

Dans le cas des fluides compressibles, il faut préciser les conditions (P,θ) pour connaître l’expression de ρ. Les gaz sont des fluides compressibles.

Dans tout le cours on s’intéressera uniquement à des liquides qui seront assimilés à des fluides incompressibles ce qui constitue une approximation excellente. Il est parfois possible sans trop d’erreurs d’assimiler les gaz à des fluides incompressibles quand les variations de pression sont faibles tout au long de l’écoulement.

2 / Conservation de la matière, débit et vitesse d’un liquide

Le débit d’un liquide est le volume (débit volumique) ou la masse (débit massique) de liquide traversant une section donnée d’une canalisation pendant l’unité de temps choisi (heure, minute, seconde …). Les unités pourront donc être: m³.h^-1, m³.s^-1, kg.s^-1 ...

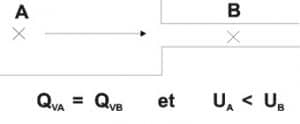
Par suite de la conservation de la matière entre deux points A et B d’un écoulement, les débits massiques sont identiques entre les deux points. En ajoutant l’hypothèse de fluide incompressible, on montre donc que les débits volumiques sont constants le long de l’écoulement.

QmA = QmB ⇔ ρA ⋅QVA = ρB ⋅QVB ⇒ QVA = QVB car ρA = ρB

Le débit Q_V (m³.s^-1), la vitesse moyenne du liquide U_m (m.s^-1)  et la section S (m²)  de la canalisation sont reliés par la relation suivante :

Q_V = U_m ⋅S

On retient ce résultat général pour tous les liquides:

Le débit volumique (ou massique) d’un liquide est identique en tous points d’une canalisation où le liquide circule. La canalisation peut présenter des différences de diamètres, le débit volumique sera toujours identique. Seule la vitesse du liquide va varier: elle augmente quand la section de canalisation diminue et inversement.

La vitesse du liquide au contact de la paroi est nulle; la vitesse atteint son maximum sur l’axe de la canalisation.

remarque:  dans tout le cours les canalisations sont supposées cylindriques. Si les canalisations ne le sont pas il faut dans les formules remplacer le diamètre D par le diamètre hydraulique D_h défini par:

 

D_h =4.S / Pér

 

où S et P sont respectivement la section de passage du liquide et Pér le périmètre mouillé par le liquide. On retrouve d’ailleurs avec cette définition le diamètre “habituel” pour un cercle.

Dans la suite la vitesse U représente la vitesse moyenne U_m.

3 / Charge d’un liquide en un point

La charge d’un liquide en un point A d’une canalisation représente en fait l’idée de la quantité d’énergie “contenue” par un liquide en ce point. Cette énergie peut aussi s’exprimer en unité de pression ou en unité de longueur (hauteur de liquide circulant équivalente à la mesure de pression).

remarque:  une pression correspond à une énergie par unité de volume tandis qu’une longueur correspond à une énergie par unité de poids

Elle est composée de trois termes correspondant respectivement à l’énergie due aux forces de pression, à l’énergie potentielle et à l’énergie cinétique du liquide. On a donc les expressions suivantes:

P_A, U_A et z_A représentent respectivement la pression en A (Pa), la vitesse en A ( m/s) et l’altitude de A (m) par rapport à un niveau zéro de référence.

L’expression en unité de longueur est appelée la hauteur manométrique en A (h_A)  ou la charge totale du liquide en A.

4 / Viscosité dynamique d’un liquide

On considère deux plaques planes et parallèles séparées par une mince couche de liquide. La plaque inférieure est maintenue au repos et la plaque supérieure se déplace d’un mouvement de translation uniforme de vitesse u. Les différentes couches de liquide sont entraînées par le mouvement de la plaque à des vitesses différentes selon leur position par rapport à la plaque mobile.

Des forces de résistance au déplacement apparaissent entre les différentes couches de liquide (analogie avec les frottements des solides) : elles sont dues à la viscosité du liquide. La force de résistance F au glissement des couches dépend de la nature du liquide et donc de sa viscosité. Elle n’existe que pour un liquide en mouvement. On donne l’expression du module de cette force s’exerçant sur une surface S parallèlement à la vitesse du liquide mais en sens contraire (signe -)

5 / Notion de perte de charge

On appelle fluide parfait un fluide pour lequel la viscosité dynamique est nulle. Ce modèle physique ne correspond pas à la réalité mais constitue un cas limite pouvant parfois être utilisé pour une première approche (on verra dans la suite qu’on applique en fait ce modèle chaque fois que les pertes de charge sont négligées).

Tous les liquides ont en fait une certaine viscosité; lors du déplacement des liquides des frottements apparaissent entre les différentes couches de liquide ou contre les parois de la canalisation ou d’un accident. Ces frottements entraînent donc une production de chaleur correspondant à une perte d’énergie pour le liquide. On parle de pertes de charge.

Pour une canalisation horizontale cette perte d’énergie se caractérise par une diminution de la pression dans le sens de l’écoulement.

Les pertes de charge sont un élément fondamental de l’écoulement des liquides car elles apparaissent pour tous les liquides. Elles se classent en deux types :

•  les pertes de charge dues aux simples frottements décrits plus haut : ce sont les pertes de charge générales dues à la seule présence d’une canalisation rectiligne sans accident.
•  les pertes de charge provoquées par la présence d’accidents sur la canalisation : rétrécissement, élargissement, vanne, coude, clapet, filtre, débitmètre,  échangeur … Ces accidents provoquent également des pertes d’énergie sous forme de frottements à cause des tourbillons créés par ces obstacles. On les nomme pertes de charges locales ou singulières.

III/ CONSERVATION DE L’ÉNERGIE

On considère une canalisation de A vers B comportant une pompe et plusieurs accidents. Le liquide circulant à l’intérieur est un fluide réel: des pertes de charge apparaissent donc automatiquement. La pompe constitue un apport d’énergie pour le liquide.

On veut écrire la conservation de l’énergie entre les points A et B du liquide; on écrit d’ordinaire cette conservation en utilisant les unités de longueur puis les unités de pression (on a vu que ces unités étaient représentatives de l’énergie). Par conséquent on notera J_A→B le terme de perte de charge en m (perte d’énergie) et Hmt (hauteur manométrique totale) le terme représentatif de la pompe en m (gain d’énergie). Hmt représente l’augmentation de la charge du liquide due à l’intervention de la pompe.

Les deux dernières relations sont les expressions généralisées de l’équation de Bernoulli.

Les différentes formes d’énergie du liquide sont susceptibles de se transformer le long de l’écoulement (transformation d’énergie de pression en énergie cinétique par exemple et inversement). En absence de pompe et en négligeant les pertes de charge entre A et B, les charges en A et B sont identiques: seules les valeurs relatives des trois termes d’énergie ont pu varier.

On remarque qu’en absence de pompe, la perte de charge entre A et B est la différence de charge entre A et B soit h_A – h_B.

IV  CALCUL DES PERTES DE CHARGE

1 / Régimes d’écoulement

Si on injecte un petit volume de colorant dans l’axe d’une canalisation horizontale parcourue par de l’eau, on observe suivant le débit du liquide (c’est-à-dire suivant sa vitesse puisque la section est constante) les phénomènes suivants:

 

• faibles débits: la trajectoire du filet de colorant est rectiligne. Les couches de liquide s’écoulent concentriquement les unes sur les autres sans qu’il y ait de mélange.

 

→ le régime d’écoulement est dit laminaire

• forts débits: le colorant se mélange rapidement à l’eau par création de mouvements tourbillonnaires. Les forces dues à la viscosité ne sont alors plus suffisantes pour empêcher la naissance d’une multitude de tourbillons.

→ le régime d’écoulement est dit turbulent

Pour distinguer quantitativement les deux types de régimes observés, on utilise un critère basé sur le nombre de Reynolds Re (nombre sans unité ou adimentionnel):

où µ, D, U et ρ sont respectivement la viscosité dynamique du liquide (en Poiseuils), le diamètre de la canalisation (m), la vitesse du liquide (m.s^-1)  et la masse volumique du liquide (kg.m^-3).

On définit les régimes d’écoulement suivants:

Re < 2000: régime laminaire        Re > 3000: régime turbulent

Entre ces deux valeurs de Re, le régime est qualifié d’intermédiaire.

Le profil des vitesses suivant la section est une parabole pour le régime laminaire (U_m = 0,5 . U_max)  ; par contre, pour le régime turbulent, le profil montre un aplatissement au centre de la canalisation (U_m = 0,8 . U_max).

On retiendra les points suivants:

• le régime turbulent est favorisé par les éléments suivants:

∗ un débit de liquide élevé

∗ un faible diamètre de canalisation

• quand le régime est turbulent, les frottements augmentent donc la perte de charge augmente dans une canalisation.

En conclusion, il faut retenir que dans les applications industrielles courantes c’est le régime turbulent qui s’applique. Le régime laminaire est observé seulement pour des liquides très visqueux.

remarque:  pour un écoulement turbulent, il existe toujours au voisinage de la paroi une mince couche de liquide où l’écoulement est laminaire. L’épaisseur de la couche diminue si la vitesse moyenne dans la canalisation augmente. Cette couche intervient de manière très importante dans les échanges thermiques par convection.

2 / Calcul des pertes de charge générales

Expérimentalement on constate que les perte de charge générales dépendent des éléments suivants :

• Longueur de la canalisation : la perte de charge est logiquement directement proportionnelle à la longueur de la canalisation ; elle augmente quand la longueur de canalisation augmente.
• Viscosité du liquide : plus le liquide est visqueux, plus les frottements donc la perte de charge augmente.
• Diamètre intérieur : quand le diamètre diminue, la perte de charge augmente considérablement. Le liquide a plus de difficultés à s’écouler donc les frottements augmentent pour un débit identique.
• Débit : plus le débit augmente, plus les forces de frottements augmentent pour un diamètre identique.
• Rugosité de la canalisation : la rugosité correspond à la notion habituelle de présence plus ou moins importante d’aspérités sur une surface. On constate ici que lorsque la rugosité d’une canalisation augmente les frottements seront plus nombreux donc la perte de charge augmentera. La perte de charge est donc fonction du matériau de la canalisation.

D’autres abaques permettent de trouver directement pour un liquide et un type de canalisation (diamètre, rugosité et liquide donnés) la perte de charge en m de liquide circulant par mètre de canalisation en fonction du débit et du diamètre ; il s’agit alors de la perte de charge unitaire (linéique).

3/ Calcul des pertes de charge singulières

Elles sont déterminées à partir de formules empiriques ou à partir d’abaques.

La perte de charge entre deux points A et B encadrant un accident est donnée par la relation suivante exprimée en Pascals :

Où K est un coefficient (sans unité) dépendant du type d’accident. D, p et Qv sont respectivement le diamètre intérieur de la canalisation (m), la masse volumétrique du liquide (kg/m3) et le débit du fluide (m3/s).

On constate que les pertes de charge par accidents dépendent du débit et du diamètre de la même manière que les pertes de charge générales :

• Débit : une augmentation de débit provoque une augmentation des pertes de charge
• Diamètre : une augmentation de diamètre (coude, orifice de vanne) provoque une diminution des pertes de charge.

Le coefficient K est caractéristique de l’accident : il faut retenir que la perte de charge augmente quand ce coefficient augmente. On observe logiquement que par exemple le coefficient augmente si l’angle d’un coude augmente ou si la variation de diamètre est plus importante dans le cas d’un rétrécissement.

L’utilisation d’abaques est fréquente pour déterminer la perte de charge locale ; ces abaques permettent de trouver pour un accident et un débit donnés la longueur équivalente de canalisation Leq de même diamètre produisant la même perte de charge.

D’autres abaques fournissent la valeur des coefficients K en fonction  du type d’accident et des caractéristiques de cet accident (angle d’un coude par exemple).

Une autre expression de ces pertes de charge est possible avec les nombres de diamètre N définis pour un accident par :

4/ Calcul des pertes de charge totales d’un circuit  hydraulique

La perte de charge totale J d’une canalisation est donc donnée par l’expression suivante si on utilise les longueurs équivalentes de canalisation :

Des formules empiriques ou des abaques sont utilisées pour avoir des ordres de grandeur corrects des pertes de charge : il est bien entendu que des calculs très précis sont inutiles, car les installations sont toujours dimensionnées avec un coefficient de sécurité permettant une adaptation à des fonctionnements imprévus.

En conclusion, pour diminuer l’ensemble des pertes de charge dans une canalisation, afin de diminuer les coûts de fonctionnement dus aux pompes, il faut :

• diminuer la longueur de canalisation
• diminuer le nombre d’accidents sur la canalisation
• diminuer le débit de circulation
• augmenter le diamètre des canalisations
• faire circuler des liquides le moins visqueux possible
• utiliser des matériaux de faible rugosité

Il est néanmoins évident que le procédé de fabrication impose parfois des contraintes d’ordre supérieur (viscosité élevée des produits utilisés, débits forts imposés…).

V/ LES POMPES

1/ Généralités

Il existe certes des moyens de faire circuler des liquides sans l’aide de pompe ; l’utilisation de la gravité, du monte-jus fonctionnant à l’aide du vide ou de pression d’air est pratique mais limitée. L’utilisation des pompes s’impose pour des transferts de liquides à des débits élevés, à des débits réguliers, à des hauteurs élevées du sol ou à longue distance.

On distingue le montage d’une pompe en charge (réservoir d’aspiration au-dessus de la pompe) et le montage d’une pompe en aspiration (réservoir d’aspiration sous la pompe).

Quelques termes sont importants à définir :

• Les points d’entrée du liquide dans la pompe est l’orifice d’aspiration : la pression d’aspiration est mesurés en ce point.
• Le point de sortie du liquide de la pompe est l’orifice de refoulement : la pression de refoulement est mesurée en ce point.
• La partie du circuit avant l’orifice d’aspiration est le circuit d’aspiration.
• La partie du circuit après l’orifice de refoulement est le circuit de refoulement.
• La perte de charge totale dans le circuit J est égale à la somme de la perte de charge dans le circuit d’aspiration et de la perte de charge dans le circuit de refoulement.

Une pompe permet de vaincre entre les deux extrémités d’un circuit :

• Une différence de pression (remplir un réservoir sous une pression plus élevée que le réservoir de départ)
• Une différence d’altitude (remplir un réservoir à un niveau élevé au-dessus du sol)
•  Une perte de charge due à la longueur de la canalisation mais aussi à la présence des coudes, des vannes…

L’utilisation d’une pompe va permettre d’apporter l’énergie c’est à dire d’augmenter la charge du fluide en transformant l’énergie électrique ou thermique fournie au moteur de la pompe en énergie mécanique. La pompe restitue alors cette énergie sous forme d’énergie mécanique (hydraulique) pour le liquide.

On peut facilement déterminer expérimentalement la hauteur manométrique totale d’une pompe dans un circuit grâce à la relation :

2/ Courbe de réseau et point de fonctionnement

La hauteur manométrique totale fournie par une pompe est une fonction du débit de liquide circulant : elle diminue toujours quand le débit augmente.

Le circuit proposé nécessite un apport d’énergie constitué par une pompe : suivant le débit souhaité la hauteur manométrique total nécessaire aura une valeur différente : il est évident qu’elle devra augmenter si on décide de fonctionner avec un débit plus important. Cette courbe obtenue est la caractéristique du réseau : elle dépend uniquement du circuit et elle peut être déterminée avec la relation théorique donnée à partir de la relation de Bernoulli.

Le point de fonctionnement de la pompe est l’intersection de la caractéristique de la pompe et de la caractéristique du réseau : fixer un débit impose automatiquement la valeur manométrique totale.

Avec une pompe centrifuge équipée d’un variateur de vitesse à chaque vitesse correspond une caractéristiques différente. Pour un réseau donné, on peut augmenter le débit en augmentant la vitesse de rotation du moteur : la Hmt nécessaire est alors plus élevée. Par contre si on interpose sur la canalisation un filtre, la perte de charge s’accroît ce qui modifie la courbe de réseau. Le débit fourni par la pompe est alors plus faible.

3/ Puissances et rendement

La puissance hydraulique (mécanique) fournie au liquide peut se retrouver à partie de la relation de Bernouilli exprimée en unités de longueur qui doit être exprimée en unités de puissance. On applique par exemple la transformation au terme d’énergie potentielle z. Si on multiplie z par m.g, le produit m.g.z constitue une énergie (m est une masse de liquide). Il reste à diviser ce produit par une durée t pour aboutir à une puissance. On obtient donc :

Le terme z a donc été en définitive multiplié par Qv.p.g. Si on applique au terme Hmt de la pompe le même facteur, on en déduit alors l’apport énergétique due à la pompe : la puissance fournie au liquide par la pompe P hyd est alors :

P hyd = Qv.p.g.Hmt

Si on note P abs la puissance fournie au moteur de la pompe (puissance consommée), le rendement global r de la pompe est :

4/ Cavitation d’une pompe

a/ Description du phénomène

La cavitation est la vaporisation du liquide contenu dans la pompe quand il est soumis à une pression inférieure à la tension de vapeur correspondant à sa température.

Des bulles apparaissent dans les zones où la pression est le plus faible (entrée des aubes de roue des pompes centrifuges) : elles sont transportées dans les zones de pressions plus fortes où se produit leur condensation. Des implosions se produisent alors à des fréquences élevées et créent des sur pressions locales très importantes (jusqu’à des centaines de bars).

La cavitation est un phénomène à éviter absolument, car il entraîne de graves conséquences :

• érosion du matériau pouvant aller jusqu’au perçage des aubes de turbine des pompes centrifuges
• Augmentation du bruit et des vibrations générés par la pompe
• Chute des performances des pompes avec diminution importante de la hauteur manométrique totale, du débit et du rendement.

b/ Expression de la condition de non cavitation

En appliquant la relation Bernoulli entre la surface du réservoir d’alimentation et le point d’aspiration de la pompe, on parvient à la relation suivante :

En fait la condition écrite plus haut n’est pas assez restrictive ; il ne suffit pas d’écrire que la pression à l’orifice d’aspiration de la pompe soit supérieure à la tension de vapeur.

En effet, il existe des zones à l’intérieur de la pompe où la pression est encore plus faible. Pour les pompes centrifuges cet endroit se situe dans le prolongement de l’arbre. Cette pression n’est plus calculable par l’utilisateur car elle dépend de la perte de charge entre l’aspiration et ce point : elle dépend donc des caractéristiques de la pompe et augmente avec le débit.

Le problème consiste maintenant à définir un critère permettant de savoir si le risque de cavitation existe dans un circuit donné. On définit donc comme grandeur le N.P.S.H. (Net Positive Succion Head) du circuit ou N.P.S.H disp (Net Positive Succion Head disponible) par la relation suivante :

De sont côté le constructeur fournit une autre courbe caractéristique en fonction du débit : le N.P.S.H. req (Net Positive Succion Head requis) qu’il a déterminé après essais pour prendre en compte les pertes de charge de la pompe. Cette grandeur est celle permettant un fonctionnement sans risque de cavitation.

Il n’y a pas de cavitation si N.P.S.H. disp > N.P.S.H. req

On prend généralement une sécurité supplémentaire d’environ 1 m.

Remarque : la démonstration du b/ et la valeur N.P.S.H. disp sont valables pour un montage en aspiration ou en charge.

Pour déterminer la possibilité de cavitation on voit donc qu’on fait appel à la fois :

• à des éléments du circuit d’aspiration :

1. 1. montage de la pompe (charge ou aspiration)
   2. distance verticale entre la pompe et le réservoir
   3. pression au-dessus du réservoir de départ
   4. longueur de canalisation et accidents

• au fluide : température
• à la pompe : N.P.S.H. req

Il est fondamental de remarquer que le circuit de refoulement n’intervient pas dans les problèmes de cavitation ; une conséquence importante est qu’il ne faut jamais placer de vannes de réglages sur le circuit d’aspiration (elles sont susceptibles en fonction de la régulation de se fermer pratiquement ce qui crée une forte augmentation de la perte de charge sur l’aspiration) mais préférer dans le même but un positionnement sur le circuit de refoulement.

En conclusion, on peut dresser une liste de conseils à respecter, si le procédé le permet, pour éviter la cavitation :

• préférer si possible les montages de pompes en charge
• éviter de transporter des liquides à des températures trop élevées
• éviter une alimentation à partir d’un réservoir sous pression réduite
• diminuer les perte de charge du circuit d’aspiration

Si ces conseils ne peuvent être appliqués en raison des exigences du procédé, il ne reste plus qu’à trouver une pompe dont les caractéristiques montrent des valeurs de N.P.S.H. req suffisamment faibles.

Remarque 1 : 

Dans les calculs visant à rechercher la Hmt d’une pompe nécessaire on suppose toujours que la perte de charge est nulle dans la pompe ce qui est physiquement faux. En fait la valeur de la Hmt trouvée (comme la Hmt de la caractéristique donnée par le constructeur) prend en compte les pertes de charge à l’intérieur de la pompe qui sont ainsi déjà déduites d’une “Hmt théorique” supérieure qui existerait en l’absence de pertes de charge. La Hmt calculée est donc égale à la “Hmt théorique” moins la perte de charge à l’intérieur de la pompe, les deux termes de la différence étant impossible à connaître pour l’utilisateur.

Remarque 2 :

Le calcul de la condition de non cavitation peut être aussi utilisé pour rechercher la profondeur maximale Hmax à laquelle une pompe peut aspirer un liquide d’un puits. Cela revient en effet à rechercher à quelle condition seulement le liquide est présent à l’aspiration sans bulle de gaz. La condition s’écrit aussi P asp > P° (q). Si on néglige le risque de cavitation de la pompe, le terme cinétique et les pertes de charge, on peut déterminer Hmax.

Donc l’aspiration de l’eau par une pompe ne sera possible à 20°C qu’à une profondeur maximale de 10,1 m et encore dans les conditions les plus favorables. Il est important de noter que cette profondeur ne dépend absolument pas de la qualité de la pompe car il s’agit d’une limite physique. Les solutions technologiques adoptées pour s’affranchir de cette limite sont d’utiliser des pompes étagées le long de la descente ou de placer une pompe immergée au fond du puits.

5/ Caractéristiques d’une pompe

Les constructeurs fournissent les caractéristiques des pompes en fonction du débit (souvent en m3/h) pour des conditions données (nature du liquide, vitesse du moteur pour une pompe centrifuge ou fréquence et course du piston pour une pompe à membrane). Une caractéristique de pompe dépend uniquement de la construction de la pompe.

Les caractéristiques fournies sont la hauteur manométrique totale , la puissance consommée par le moteur (kw), le rendement et le N.P.S.H. req

La Hmt permet le choix de la pompe pour une courbe de réseau imposée

Le N.P.S.H.req permet en fonction des caractéristiques du circuit d’aspiration de connaître la valeur limite de débit avec laquelle la pompe peut fonctionner sans risque de cavitation.

Le rendement renseigne sur la zone de débit où le rendement est plus élevé : ainsi, il peut être économiquement avantageux de se placer à un débit plus faible (si bien sûr celui-ci n’est pas imposé par le procédé) en augmentant artificiellement la perte de charge sur le circuit de refoulement (utilisation d’une vanne de réglage).

La puissance consommée pour un débit donné permet de connaître le coût de fonctionnement de la pompe.

6/ Couplage des pompes

Pour parvenir à obtenir certaines conditions de fonctionnement impossibles à réaliser avec une seule pompe, les utilisateurs associent parfois deux pompes dans des montages en série ou en parallèle.

On considère deux pompes P1 et P2 ayant des caractéristiques différentes.

a/ Couplage en série

Les pompes P1 et P2 montées en série sont traversées par le même débit de liquide Qv. A un débit donné, la hauteur manométrique totale de ce couplage Hmt série est la somme des hauteurs manométriques totales Hmt1 et Hmt2 des deux pompes fonctionnant séparément à ce même débit :

Hmt série = Hmt1 + Hmt2

Graphiquement, on trouve la caractéristique de la hauteur manométrique totale du montage en additionnant les caractéristiques de chaque pompe pour un même débit.

Le couplage en série permet d’augmenter fortement la hauteur manométrique totale : il convient donc bien pour un réseau présentant des pertes de charge importantes.

b/ Couplage en parallèle

Les pompes P1 et P2 montées en parallèle montrent la même hauteur manométrique totale Hmt.

Graphiquement, on trouve la caractéristique de la hauteur manométrique totale du montage en additionnant les débits des deux pompes pour une même hauteur manométrique totale.

En réalité ceci n’est pas tout à fait juste. Les deux pompes n’étant jamais totalement équivalentes, la somme des débits des pompes utilisées séparément pour une Hmt fixée est inférieure au débit total Qv obtenu par couplage à cette même Hmt. Une des pompes a toujours tendance à “freiner” le liquide au  refoulement de l’autre pompe ; cette tendance peut aller jusqu’à entraîner la rotation de la pompe en sens contraire. Les pompes sont souvent équipées d’un clapet anti-retour sur la canalisation de refoulement pour éviter le retour de liquide au refoulement d’une des pompes.

Le couplage en parallèle permet d’augmenter le débit dans le réseau : il convient bien pour un réseau présentant des pertes de charge assez faibles. Les pompes sont parfois montées en parallèle (by-pass) avec une seule des deux fonctionnant. En cas de panne ou pour une action de maintenance le montage permet alors de continuer à fonctionner en démarrant la deuxième pompe.

c/ Intérêt des couplages

Le couplage de pompe n’est pas forcément avantageux pour le coût de fonctionnement de l’installation : autrement dit, une “grosse” pompe est souvent plus économique que l’association en série de deux “petites” pompes. Il faut donc examiner chaque cas particulier avant de trancher. Il faut de plus éviter la généralisation : on peut montrer parfois que pour un réseau présentant de fortes pertes de charge, le couplage en série permet un débit plus important que celui en parallèle.

Concernant les pompes centrifuges, l’utilisation de pompes centrifuges multicellulaires est préférée à l’utilisation en série de plusieurs pompes centrifuges.

VI/ CHOIX D’UNE CANALISATION ET D’UNE POMPE

Le choix du diamètre et du matériau d’une canalisation doit être adapté au liquide ou à la suspension qui doit le parcourir. Un liquide corrosif ne pourra être véhiculé par une canalisation en acier ordinaire. On devra choisir le diamètre pour l’écoulement d’une suspension de telle manière que la vitesse d’écoulement ne soit pas inférieure à 0.3 -0.6 m.s -1 pour éviter le dépôt de particules. De même la vitesse ne pourra être supérieure à 4-5 m.s-1 afin d”éviter une usure trop rapide de la conduite.

Dans l’industrie, la vitesse des liquides dans les canalisations est pratiquement toujours comprise entre 0,5 et 5 m.s-1

Connaissant le débit qu’on souhaite utiliser, le choix de la vitesse d’écoulement et par suite du diamètre découle de la recherche d’un optimum économique. Un diamètre plus grand entraîne un investissement plus important mais se traduit par une perte de charge plus faible et donc des frais de fonctionnement plus bas.

Le choix d’une pompe va résulter en premier lieu d’une analyse des éléments du circuit (différence d’altitude, pressions des réservoirs, nature et température du liquide, présence d’accidents, matériau et caractéristiques géométriques de la canalisation). Cette analyse va permettre de déterminer la hauteur manométrique totale nécessaire pour le débit souhaité ainsi que le N.P.S.H. disp. 

L’utilisation des caractéristiques des pompes fournies par le constructeur intervient alors pour choisir une pompe remplissant toutes les exigences.

ANNEXE 1

COUP DE BÉLIER

Lorsqu’un liquide circule dans une canalisation à une vitesse de quelques mètre par seconde (vitesse habituelle dans une canalisation), il se produit dans certaines circonstances le phénomène du coup de bélier. C’est le cas notamment de la fermeture brusque d’une vanne ou de l’arrêt d’une pompe. Ces événements peuvent correspondre à des manœuvres normales sur la canalisation ou à des incidents (panne d’une pompe, erreur de manipulation des vannes).

L’interruption rapide d’un écoulement nécessite l’intervention de forces de pression très importantes. Des ondes mécaniques apparaissent dans les canalisations avec des phénomènes de réflexion sur les accidents de la canalisation. Les effets sont particulièrement néfastes pour les tuyaux qui ne peuvent supporter des variations de pressions trop importantes.

Pour remédier aux coups de bélier, on peut utiliser des vannes à fermeture lente (on remédie à la cause du coup de bélier) ou des réservoirs antibéliers qui permettent une diminution de leurs effets. Ceux-ci communiquent avec un point de la canalisation et sont placés au-dessus d’elle. Il sont constitués par une capacité remplie partiellement de liquide et dont la partie haute sous pression d’air. Les variations de pression dans le tuyau sont donc amorties par les variations de volume de la partie remplie d’air.

ANNEXE 2

ANALOGIE ELECTRIQUE

Entre deux points d’un circuit électrique ou hydraulique, on peut faire l’analogie entre une différence de potentiel et une différence de pression. Le débit de liquide a son équivalent avec l’intensité qui est un débit de charges électriques.

La détermination du point de fonctionnement à l’aide des caractéristiques de la pompe et du réseau a son équivalent en électricité. Si on considère un générateur (producteur d’énergie) avec une résistance interne, sa caractéristique tension – intensité est l’équivalent de celle de la pompe en fonction du débit.

La caractéristique d’une résistance électrique (la résistance provoque une perte d’énergie) est l’équivalent de la caractéristique du réseau avec les pertes de charge.

Le point de fonctionnement du circuit électrique est l’intersection des caractéristiques du générateur et de la résistance.